分数分子加1,分母不变,分数值会怎么变?
有一个分数分子加上1,看似一个简单的数学操作,却能在数学的多个领域中引发一系列有趣且深刻的连锁反应,这个操作不仅改变了分数本身的数值,更可能影响其在不等式、方程、函数乃至实际应用中的表现,让我们深入探讨这一操作在不同情境下的意义和影响。
从最基本的数值变化来看,对于一个正分数(分子和分母均为正整数),当分子加上1时,分数的值必然增大,这是因为分子是分数的“被除数”,增加被除数而除数不变,商自然会变大,分数1/2,分子加1后变为2/2,即1,数值从0.5增加到1;再如3/4,分子加1后为4/4,即1,数值从0.75增加到1,如果原分数的分子已经大于或等于分母,即假分数,那么分子加1后,分数的值同样增大,但其整数部分可能会增加,例如5/3约等于1.666,分子加1后为6/3,即2,整数部分从1增加到2,对于负分数,情况则相反,若分数为负(如-1/2),分子加1后变为0/2,即0,数值从-0.5增加到0;若分数为-3/4,分子加1后为-2/4,即-1/2,数值从-0.75增加到-0.5,可见,分子加1对分数值的影响,取决于分数本身的符号。
在不等式领域,分子加1的操作会改变不等式的方向或强弱,考虑一个简单的不等式:a/b < c,其中a、b、c为正数,如果我们对左边的分数分子加1,得到(a+1)/b,那么新的不等式(a+1)/b < c是否成立,取决于a+1与b*c的关系,1/3 < 1,显然成立;分子加1后,2/3 < 1,仍然成立,但如果原不等式是2/3 < 1,分子加1后3/3=1,不等式1 < 1就不成立了,变成了等式,这表明,分子加1可能会使一个原本成立的不等式变得不成立,或者从一个严格不等式变为非严格不等式,在更复杂的不等式中,如比较两个分数的大小,分子加1会直接影响比较结果,比较1/2和2/3,显然1/2 < 2/3;若对第一个分数分子加1,得到2/2=1,则1 > 2/3,在处理含有分数的不等式时,对分子进行加1操作需要极其谨慎,必须重新评估整个不等式的成立条件。
在方程中,分子加1会改变方程的解,假设我们有一个方程如x/(x+1) = 1/2,解这个方程可以得到x=1,如果我们对方程左边的分数分子加1,方程变为(x+1)/(x+1) = 1/2,即1 = 1/2,这是一个无解的矛盾方程,可见,分子加1可能彻底改变方程的性质,使其从有解变为无解,或者解发生根本性变化,在分式方程中,分母通常不能为零,分子加1虽然不直接改变分母(除非分子加1的表达式与分母有关联),但可能会引入新的限制或消除原有的限制,方程1/(x-1) = 2,x不能为1;若分子加1变为2/(x-1)=2,解为x=2,此时x=1仍然不是解,但解的值发生了变化。
在函数研究中,分数函数的分子加1相当于对函数进行了一次变换,考虑函数f(x) = 1/x,其图像为双曲线,如果我们定义一个新的函数g(x) = (x+1)/x = 1 + 1/x,这相当于将f(x)的图像向上平移1个单位,这种平移变换改变了函数的值域、渐近线等性质,原f(x)=1/x的值域为y≠0,渐近线为x=0和y=0;而g(x)=1+1/x的值域为y≠1,渐近线变为x=0和y=1,可见,分子加1(这里的分子是变量x)对函数图像和性质的影响是系统性的,对于更复杂的分数函数,如h(x) = (2x+3)/(x-1),分子加1后变为k(x) = (2x+4)/(x-1) = 2 + 6/(x-1),这同样改变了函数的表达式和图像特征。
在实际应用中,分数常用来表示比例、概率、效率等,分子加1可能对应着“增加一个单位”的实际含义,一个产品合格率为98/100,即98%,如果分子加1,变为99/100,即99%,表示合格率提升了一个百分点,再如,一个班级有30名学生,其中20名是女生,女生比例为20/30=2/3;如果转来1名女生(分子加1,分母也加1),则比例为21/31≈67.7%,此时比例的变化不仅与分子加1有关,还与分母的变化相关,但若题目仅限定“分子加上1”,则分母不变,如20/30变为21/30=7/10=70%,表示女生人数增加1人,总人数不变时的比例变化,这种变化在实际决策中具有重要意义,如质量控制、资源分配等。
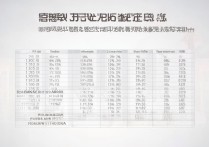
为了更直观地展示分子加1对不同分数的影响,我们可以通过表格来对比:
| 原分数 | 分子加1后的分数 | 原分数值(小数) | 新分数值(小数) | 值的变化趋势 |
|---|---|---|---|---|
| 1/2 | 2/2=1 | 5 | 1 | 增加 |
| 3/4 | 4/4=1 | 75 | 1 | 增加 |
| 5/3 | 6/3=2 | ≈1.666... | 2 | 增加 |
| -1/2 | 0/2=0 | -0.5 | 0 | 增加(负变零) |
| -3/4 | -2/4=-1/2 | -0.75 | -0.5 | 增加(负值变大) |
| 0/5 | 1/5 | 0 | 2 | 增加 |
从表格中可以清晰地看到,无论是正分数、负分数还是零分子分数,分子加1后,其数值均呈现“增加”的趋势,尽管负分数的“增加”实际上是向零靠近或负值绝对值减小。
“有一个分数分子加上1”这一简单的数学操作,绝非简单的数值叠加,它在不同数学分支和应用场景中扮演着多重角色,引发一系列复杂而有序的变化,理解这一操作对分数值、不等式、方程、函数以及实际应用的影响,有助于我们更深刻地把握分数的本质及其在数学体系中的纽带作用。
相关问答FAQs:
问题1:如果一个真分数的分子加上1,其值一定会大于原分数吗?是否存在例外?
解答:对于一个真分数(分子小于分母的正分数),当分子加上1时,其值一定会大于原分数,不存在例外,这是因为真分数的分子和分母均为正数,且分子 < 分子,分子加1后,新的分子为原分子+1,显然大于原分子,而分母不变,根据分数的基本性质,分子越大,分数值越大(分母为正时),2/5是真分数,分子加1后为3/5,3/5 > 2/5,即使原分子为0(如0/3,值为0),分子加1后为1/3,1/3 > 0,对于真分数而言,分子加1必然导致分数值增大。
问题2:在解分式方程时,如果对其中一个分数的分子加上1,方程的解会发生怎样的变化?需要注意什么?
解答:在解分式方程时,对其中一个分数的分子加上1,会改变方程的结构,从而可能导致方程的解发生变化,甚至使方程无解或产生增根,原方程1/(x-1) = 1/2,解为x=3;若对左边分数分子加1,变为2/(x-1) = 1/2,解为x=5,解的值发生了变化,再如,原方程x/(x+1) = x/(x+2),解为x=0;若左边分子加1,变为(x+1)/(x+1) = x/(x+2),即1 = x/(x+2),解为x=-2,此时需要检验x=-2是否使原方程(变形后)的分母为零,此处x=-2不使分母为零,是有效解,但解的值和数量都可能改变,需要注意的是,分子加1后,解方程的步骤需要重新进行,并且必须检验解是否使原方程(或变形后的方程)的分母为零,以排除增根,分子加1后,方程的解可能从有解变为无解,如(x)/(x+1) = 1,解为x无解(实际上x无解,因为x/(x+1)=1无解);若分子加1变为(x+1)/(x+1)=1,即1=1,此时方程变为恒等式,解为使分母不为零的所有实数x≠-1,解的情况发生了根本性改变,必须仔细分析分子加1后方程的具体形式,并严格检验解的有效性。
版权声明:本文由 数字独教育 发布,如需转载请注明出处。












 冀ICP备2021017634号-12
冀ICP备2021017634号-12
 冀公网安备13062802000114号
冀公网安备13062802000114号