小数和分数如何转换？它们之间有什么联系？

小数和分数是数学中两种重要的数的表现形式,它们之间存在着密切的联系，这种联系不仅体现在数值的等价性上，更体现在运算规则、实际应用以及数学概念的拓展等多个层面，理解小数和分数的联系，对于深入掌握数学知识、解决实际问题具有重要意义。

从本质上看,小数和分数都是用来表示非整数的数，它们可以表示同一个数值，只是形式不同，分数是整数扩展的结果，表示一个整体被平均分成若干份后，取其中的一份或几份，1/2表示把一个整体平均分成2份，取其中的1份，而小数则是基于十进制计数法产生的，是小数部分不足1的数的表示方法，它利用小数点将整数部分和小数部分分开，每一位上的数字代表不同的十进制位，0.5表示5个十分之一，这与1/2表示的数值是完全相同的，这种数值上的等价性是小数和分数最直接的联系，为了更清晰地展示这种联系，我们可以列举一些常见的分数和小数对应关系：1/2=0.5，1/4=0.25，3/4=0.75，1/5=0.2，2/5=0.4，1/8=0.125，1/10=0.1等等，这些例子表明，许多分数都可以转化为小数，许多小数也可以转化为分数。

小数和分数的互化是实现两者联系的关键桥梁,将分数化为小数，通常采用除法运算，即用分数的分子除以分母，将3/4化为小数，就是用3除以4，得到0.75，这里需要注意的是，根据分母的不同，分数化成小数的结果可能是有限小数，也可能是无限循环小数，如果分母中只含有2和5的因数（即分母是10的幂的因数），那么这个分数就能化成有限小数，如1/8=0.125（分母8=2³）；如果分母中含有2和5以外的质因数，那么这个分数就能化成无限循环小数，如1/3=0.333…（分母3含有质因数3），1/6=0.1666…（分母6=2×3，含有质因数3），反过来，将小数化为分数，则可以根据小数的位数来确定分母，有限小数化分数时，小数部分有几位，分母就是10的几次方，然后能约分的要约分，0.25有两位小数，分母就是100，即25/100，约分后为1/4，对于无限循环小数，其化分数的方法相对复杂一些，需要通过设未知数、列方程等步骤来解决，设x=0.333…，则10x=3.333…，两式相减得9x=3，所以x=1/3。

在运算方面,小数和分数也遵循着共同的运算定律，如交换律、结合律、分配律等，这使得它们在运算过程中可以相互转化，以简化计算，计算1/2 + 0.25，既可以先将1/2化为0.5，然后0.5+0.25=0.75；也可以先将0.25化为1/4，然后1/2+1/4=3/4，结果相同，在进行乘除法运算时，这种转化同样方便，计算0.4 × 1/5，可以将0.4化为2/5，然后2/5 × 1/5=2/25；也可以先将1/5化为0.2，然后0.4×0.2=0.08，两者都是正确的，选择将小数化为分数还是分数化为小数进行计算，通常取决于具体的问题和计算的便捷性，有时，分数形式在约分或通分时更为直观；有时，小数形式在加减法中对位更为方便。

小数和分数的联系还体现在它们在实际应用中的互补性,在日常生活中，我们经常会遇到需要使用小数或分数来表示数量的情况，在测量长度时，可能会用到0.5米（即1/2米）、0.25厘米（即1/4厘米）；在表示重量时，可能会用到1.5千克（即3/2千克）、0.75吨（即3/4吨），在金融领域，利率、折扣等常常用小数表示，如5%的利率即0.05，而某些比例关系则可能用分数表示更为贴切，如“一半”即1/2，在科学计算中，小数的精确性使其在需要高精度表示时更为常用，而分数在某些公式推导或单位换算中则能保持数值的精确性，避免小数的近似带来的误差，在圆周率π的计算中，虽然我们常用3.14、3.1416等小数近似值，但在一些精确的公式表达中，π仍然以符号形式保留，或者在分数近似（如22/7）中使用。

从数学概念的发展历程来看,分数的产生早于小数，在古代文明中，由于分配物资、测量土地等实际需求，人们开始使用分数来表示非整数，而小数的出现则是十进制计数法发展到一定阶段的产物，它的出现极大地简化了分数的运算和表示，特别是对于分母是10的幂的分数，小数的引入，使得数的表示和运算更加系统化和便捷，为数学的发展，尤其是高等数学的产生奠定了基础，可以说，小数是分数在十进制下的一种特殊且高效的表示形式，它丰富了数的概念，拓展了数的应用范围。

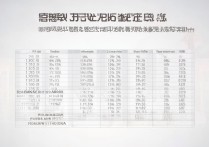
为了更直观地展示小数和分数在互化过程中的对应关系,我们可以通过一个表格来举例说明：

| 分数 | 小数（有限） | 小数（无限循环） | 备注 | | ：--- | ：----------- | :--------------- | :--- | | 1/2 | 0.5 | - | 分母含因数2 | | 1/4 | 0.25 | - | 分母含因数2² | | 1/5 | 0.2 | - | 分母含因数5 | | 1/8 | 0.125 | - | 分母含因数2³ | | 1/3 | - | 0.333… (0.3) | 分母含因数3 | | 1/6 | - | 0.1666… (0.16) | 分母含因数2和3 | | 2/3 | - | 0.666… (0.6) | 分母含因数3 | | 1/9 | - | 0.111… (0.1) | 分母含因数3² | | 1/10 | 0.1 | - | 分母含因数2和5 |

通过上表可以看出,分数能否化为有限小数，取决于其分母的质因数分解，这是小数和分数在数值性质上的一个重要联系点。

小数和分数都可以在数轴上找到对应的点,这进一步体现了它们在数轴上的统一性，1/2和0.5在数轴上对应的是同一个点；1/4和0.25也是同一个点，即使是无限循环小数，如1/3=0.333…，在数轴上也有一个确定的点，它位于0和1之间，更靠近0，且与0的距离是1/3，这种数轴上的统一性，表明小数和分数都是实数的重要组成部分，它们共同构成了连续的数轴。

在教育教学中,小数和分数的联系也是教学的重点和难点，教师通常会通过具体的实例、图形（如圆形、长方形等）的分割来帮助学生理解分数的意义，然后再引导学生将分数与小数联系起来，通过除法运算体会分数化小数的过程，反过来，通过小数的数位意义，帮助学生理解小数如何转化为分数，这种双向的转化教学，有助于学生构建完整的数的概念，避免将小数和分数割裂开来学习。

小数和分数之间存在着多方面、深层次的联系，它们在数值上等价，可以互化；在运算上遵循共同的定律，可以相互转化以简化计算；在实际应用中各有侧重又互为补充；在数学概念的发展上，小数是分数的延伸和精细化，深入理解这些联系，不仅能够帮助我们更好地掌握小数和分数的知识，提高数学运算能力和解决实际问题的能力，还能够培养我们的数学思维，体会数学知识的内在统一性和系统性。

相关问答FAQs：

问题1：为什么有些分数能化成有限小数，有些却只能化成无限循环小数？ 解答：分数能否化成有限小数，取决于其分母的质因数分解情况，当分数的分母（化为最简分数后）只含有质因数2和5时，这个分数就能化成有限小数，这是因为十进制计数法的基础是10，而10=2×5，所以分母中只有2和5的因数时，可以通过分子分母同乘以适当的数，使分母变成10的幂，从而化成有限小数，1/4的分母是4=2²，分子分母同乘以5²=25，得到25/100=0.25，如果分数的分母（化为最简分数后）含有2和5以外的质因数（如3,7,11等），那么这个分数就只能化成无限循环小数，因为这些质因数无法通过乘以整数转化为10的幂，导致除法运算过程中会出现余数重复出现的情况，从而形成循环节，1/3的分母是3，含有质因数3，所以1/3=0.333…是一个无限循环小数。

问题2：在实际计算中，什么情况下更适合将分数化为小数，什么情况下又更适合将小数化为分数？ 解答：在实际计算中，选择将分数化为小数还是小数化为分数，主要取决于运算的类型、数据的特点以及对结果精度的要求，在进行加减法运算时，如果小数的位数较少且对齐方便，或者分数的分母较大且通分困难，将分数化为小数进行计算可能更为简便，计算0.35 + 1/4，将1/4化为0.25，然后0.35+0.25=0.60，直接相加即可，而在进行乘除法运算时，如果分数的分子分母可以约分，或者小数的小数位数较多，将小数化为分数进行计算可能更为便捷，且能保持结果的精确性，计算0.25 × 2/3，将0.25化为1/4，然后1/4 × 2/3=2/12=1/6，避免了小数乘法可能带来的繁琐计算和近似误差，在需要精确表示结果，或后续运算需要利用分数的性质（如约分、通分）时，应尽量保留分数形式；而在需要快速估算、或结果要求以小数形式呈现（如货币、测量值）时，则可化为小数。